'Bài toán ghế sofa' hóc búa cuối cùng đã có lời giải sau hàng thập kỷ

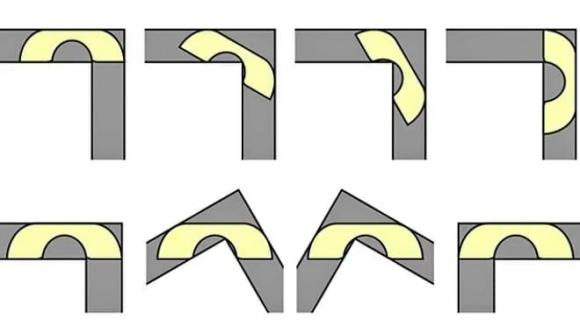
Bài toán này, gợi nhớ đến cảnh Ross vật lộn với chiếc ghế sofa mới trong sitcom nổi tiếng "Friends" (1999), yêu cầu xác định diện tích lớn nhất của một hình dạng phẳng có thể di chuyển quanh góc vuông 90 độ trong một hành lang có chiều rộng nhất định. Trong phim, Ross liên tục kêu gọi "Xoay!", nhưng có lẽ mọi chuyện đã dễ dàng hơn nếu anh biết đến "ghế sofa Gerver" - một hình dạng phức tạp với 18 đoạn cong, được cho là có diện tích tối đa 2,2195 đơn vị.

Bài toán "ghế sofa" sau hàng thập kỷ cuối cùng đã có lời giải (Ảnh minh hoạ)

Bài toán "ghế sofa" được đặt ra lần đầu tiên bởi nhà toán học người Áo-Canada Leo Moser vào năm 1966. Moser đặt câu hỏi về diện tích lớn nhất có thể của một hình dạng hai chiều có thể di chuyển quanh góc vuông của một hành lang có chiều rộng đơn vị là một. Nghe có vẻ đơn giản, nhưng bài toán này lại vô cùng phức tạp, đòi hỏi phải xem xét cả việc tối đa hóa diện tích và tính toán quỹ đạo chuyển động của hình dạng.

(Ảnh minh hoạ)

Gần đây, Jineon Baek, một nhà nghiên cứu sau tiến sĩ tại Đại học Yonsei, Hàn Quốc, đã công bố một lời giải cho bài toán hóc búa này. Trong một bản thảo dài hơn 100 trang được đăng tải trên trang web arXiv vào ngày 2 tháng 12, Baek đã đưa ra một bằng chứng toán học chỉ ra rằng diện tích tối đa của "ghế sofa" lý tưởng là 2,2195 đơn vị trong một hành lang rộng 1 đơn vị. Kết quả này đã thu hẹp đáng kể khoảng diện tích được chấp nhận trước đó, từ 2,2195 đến 2,37 đơn vị. Tuy nhiên, lời giải của Baek vẫn cần được kiểm tra và phê duyệt bởi cộng đồng toán học thông qua quá trình bình duyệt trước khi được chính thức công nhận.

"Ghế sofa Gerver", được đặt theo tên của nhà toán học Joseph Gerver, giáo sư danh dự tại Đại học Rutgers, là một hình dạng chữ U rộng với phần "ghế ngồi" được thiết kế bằng các đường cong tinh vi, cho phép nó di chuyển quanh góc vuông mà không bị mắc kẹt. Năm 1992, Gerver đã đề xuất giới hạn dưới của diện tích là 2,2195. Tuy nhiên, giới hạn trên vẫn còn gây tranh cãi. Năm 2018, một nhóm nghiên cứu sử dụng phương pháp chứng minh bằng máy tính đã đưa ra giới hạn trên là 2,37.

(Ảnh minh hoạ)

Nghiên cứu của Baek, tập trung vào việc phân tích hình học và quỹ đạo chuyển động của "ghế sofa Gerver", đã khẳng định rằng lời giải của Gerver thực sự chính xác. Kết quả này không chỉ giải quyết một bài toán toán học lâu đời mà còn minh chứng cho sức mạnh của tư duy toán học trong việc giải quyết những vấn đề tưởng chừng như đơn giản nhưng lại ẩn chứa những phức tạp bất ngờ. Mặc dù việc áp dụng thực tế của lời giải này còn hạn chế, nhưng nó mở ra những hướng nghiên cứu mới trong lĩnh vực hình học và tối ưu hóa.

Thu Hà (Theo Thuơng Hiệu và Pháp Luật)